Расчет физически нелинейных задач
Моделирование физической нелинейности материалов конструкций производится с помощью физически нелинейных конечных элементов, воспринимающих информацию из развитой библиотеки законов деформирования материалов (зависимостей ?-?). Библиотека законов деформирования позволяет учитывать практически любые физически-нелинейные свойства материала. Эта библиотека законов деформирования материала является библиотекой открытого типа и может пополняться новыми законами.
Шаговый процессор позволяет получить напряженно-деформированное состояние с учетом нелинейных эффектов как для мономатериальных, так и для биматериальных конструкций. Для последних предлагается определенный набор характеристик второго материала (армирующих включений).
Библиотека физически нелинейных конечных элементов содержит также элементы, позволяющие моделировать одностороннюю работу твердого тела и сыпучей среды - грунта на сжатие с учетом сдвига по схеме плоской деформации в соответствии с законом Кулона.
Матрица жесткости линеаризованной физически нелинейной системы формируется на основании переменных интегральных жесткостей, вычисляемых в точках интегрирования конечного элемента при решении упругой задачи на конкретном шаге. Схема численного интегрирования по области конечного элемента и набор используемых жесткостей определяются типом конечного элемента. Для того чтобы получить соответствующий набор интегральных жесткостей, сечение конечного элемента в точках интегрирования дробится на ряд элементарных подобластей. В центрах этих подобластей определяются новые значения физико-механических характеристик материала в соответствии с заданной диаграммой деформирования. На каждом шаге решается линеаризованная задача с формированием векторов перемещений, усилий и новых интегральных жесткостей по касательному модулю для последующего шага. Количество шагов и коэффициенты к нагрузке задаются пользователем. Геометрическая интерпретация шагового метода для случая одноосного растяжения (сжатия) представлена на рисунке 7.1.
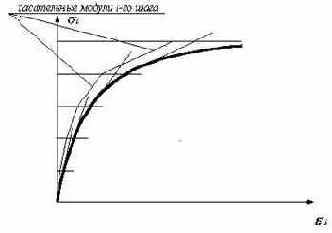
Рис. 7.1
Шаговый процессор позволяет комбинировать линейные и нелинейные конечные элементы. Допускается расчет по суперэлементной схеме, если нелинейные элементы присутствуют только в основной схеме.
На каждом шаге производится оценка напряженно-деформированного состояния. В разделе результатов расчета «Сведения о состоянии материалов» приводятся сообщения о развитии или достижении предельных состояний, появлении пластических шарниров или состояний разрушения.
Для стержневых конечных элементов анализируется напряженно-деформированное состояние поперечных сечений стержня в точках дробления. Напряженно-деформированное состояние в плоских и объемных конечных элементах анализируется в центральной точке элемента.
Библиотека физически-нелинейных КЭ содержит элементы, позволяющие производить статический анализ конструкций, состоящих из разнородных конечных элементов, с учетом физической нелинейности материала. Состав библиотеки приведен в табл. 7.1.
Таблица 7.1.
| №№ КЭ | Наименование КЭ | Признак схемы | Плос-кость располо-жения | Степени свободы |
| 1 | 2 | 3 | 4 | 5 |
| 210 (205) |
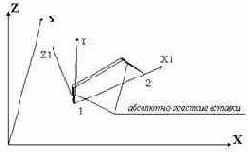
Универсальный пространственный стержневой конечный элемент - суперэлементного построения
Универсальный пространственный стержневой конечный элемент - равновесного построения
 |
1 2 3 4 5 | XOZ XOZ XOY произ-вольно | X, Z X, Z, UY X,Y,Z X,Y,Z UX, UY, UZ |
| 221 (223) |
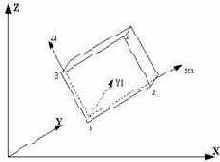
Прямоугольный элемент балки -стенки
 |
1,2,5 (4,5) | XOZ (произ-вольно) | X, Z (X,Y,Z) |
| 222 (224) |
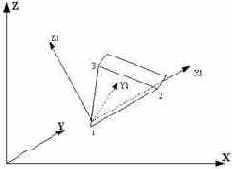
Треугольный элемент балки-стенки
 |
1,2,5 (4,5) | XOZ (произ-вольно) | X, Z (X,Y,Z) |
| 1 | 2 | 3 | 4 | 5 |
| 230 (227) |
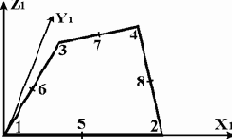
Четырехугольный (8-узловой) элемент балки-стенки
 |
1 2 (4,5) | XOZ (произ-вольно) | X, Z (X, Y, Z) |
| 231 |
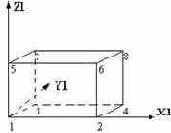
Параллелепипед
 |
4 5 | произ-вольно | X, Y, Z |
| 232 |
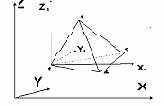
Тетраэдр
 |
4, 5 | произ-вольно | X, Y, Z |
| 233 |
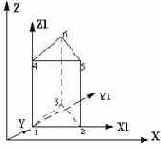
Прямая треугольная призма
 |
4 5 | произ-вольно | X, Y, Z |
| 1 | 2 | 3 | 4 | 5 |
| 234 |
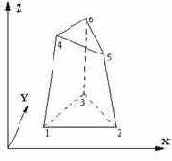
Пространственный 6-ти узловой изопараметрический элемент (произвольная треугольная призма)
 |
4 5 | произ-вольно | X, Y, Z |
| 236 |
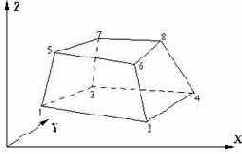
Пространственный 8-ти узловой изопараметрический элемент (произвольный гексаэдр)
 |
4 5 | произ-вольно | X, Y, Z |
| 241 |
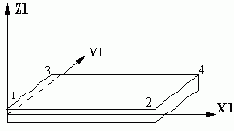
Прямоугольный элемент оболочки
 |
5 | произ-вольно | X, Y, Z, UX, UZ, UY |
| 242 |
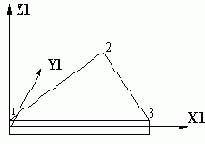
Треугольный элемент оболочки
 |
5 | произ-вольно | X,Y,Z UX,UY,UZ |
| 1 | 2 | 3 | 4 | 5 |
| 244 |
Универсальный четырехугольный конечный элемент оболочки
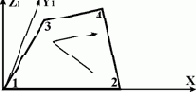 |
5 | произ-вольно | X, Y, Z, UX, UY, UZ |
| 281 |
Прямоугольный элемент грунта (плоская деформация)
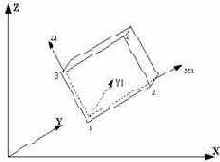 |
1,2 | XOZ | Плоская деформация X, Z |
| 282 |
Треугольный элемент грунта (плоская деформация)
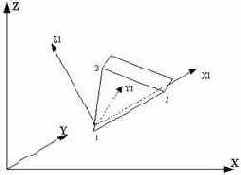 |
1,) | XOZ | Плоская деформация X, Z |
| 284 |
Четырехугольный элемент грунта (плоская деформация)
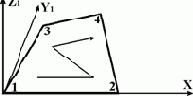 |
1 2 | XOZ | Плоская деформация X, Z |