Универсальные конечные элементы

Предназначены для решения плоской задачи теории упругости, а также прочностного расчета тонких, жестких пластин и тонких пологих оболочек. Материал однородный по толщине элемента, линейно упругий изотропный.

Тонкими считаются пластины, у которых 5 £ Lmin/ d, где Lmin - наименьший из размеров в плане; d - толщина.

Жесткими считаются пластины, у которых наибольший прогиб не превышает d/5.

Оболочки считаются тонкими, если R/d > 20, где R - минимальный радиус кривизны срединной поверхности.

Оболочки считаются пологими, если L min/fo ³ 5, где fo - стрела подъема свода оболочки.

Применительно к решению плоской задачи теории упругости, МКЭ исходит из общепринятых гипотез об отсутствии деформаций (ez, gxz., gyz = 0 для случаев плоской деформации) или напряжений (sz, txz, tyz = 0 для случая плоского напряженного состояния) в плоскостях, нормальных к срединной плоскости пластин. Функционал Лагранжа, как для плоской деформации, так и для плоского напряженного состояния имеет вид:

(1.6)

где: sx ,sy

,txy

- нормальные и касательное напряжения;

-относительные линейные и угловая деформации;

u (x, у), v (x, у) - линейные смещения точек срединной плоскости по направлению осей Х и Y соответственно;

Px, Py — компоненты вектора внешней нагрузки по направлениям осей Х и Y соответственно;

W - двумерная область пластины.

При решении задач изгиба тонких пластин, МКЭ исходит из допущений (гипотез), принятых при построении инженерной теории тонких пластин, а именно:

· гипотезы о прямых нормалях Кирхгофа-Лява (еxz = еyz = 0);

· гипотезы о вертикальном смещении точек срединной плоскости пластины;

· гипотезы об отсутствии поперечного давления (sz, = 0);

· плоское напряженное состояние.

Функционал полной потенциальной энергии изгибаемой пластины при таких допущениях и при нулевых граничных условиях имеет вид:

(1.7)

Таблица 1.3

Тип КЭ	Нагрузка	Схема и описание нагрузки	Информация, задаваемая в документах
			6."Нагрузки"		7."Величины нагрузок"
			Вид нагрузки	Направ-ление нагрузки	Величина нагрузки и привязка
1	2	3	4	5	6
21,22, 23,24, 27,30	Сосредо-точенная нагрузка в плоскости элемента XlO1Z1 (XlO1Y1)		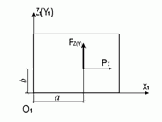5	X Z	Рх(m),a(м),b(м) Рz(m),a(м),b(м)
41,42				X Y	Рх(m),a(м),b(м) Рy(m),a(м),b(м)
21,22, 23,24		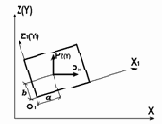	15	X Z	Рх(m),a(м),b(м) Рz(m),a(м),b(м)
41,42, 44				X Y	Рх(m),a(м),b(м) Рy(m),a(м),b(м)
11,12 41,42,44	Сосредо-точенная нагрузка из плоскости элемента - силы и моменты		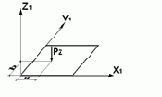5	Z UX, UY	Рz(m),a(м),b(м) M(m м),a(м),b(м)
11,12 41,42,44		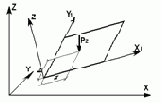	15	Z UX, UY	Рz(m),a(м),b(м) M(m м),a(м),b(м)
1	2	3	4	5	6
21,22, 23,24, 27,30	Равномерно распреде-ленная нагрузка в плоскости элемента		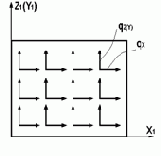6	X Z	qx(m/м2) qz(m/м2)
41,42, 44				X Y	qx(m/м2) qy(m/м2)
21,23, 27,30		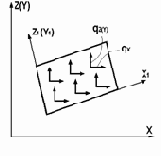	16	X Z	qx(m/м2) qz(m/м2)
41,44				X Y	qx(m/м2) qy(m/м2)
11,12 41,42, 44	Равномерно распреде-ленная нагрузка из плоскости элемента - силы и моменты по площади		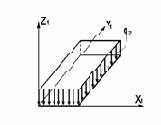6	Z UX UY	qz(m/м2) mx(mм /n.м) my(mм /n.м)
11,12 41,42, 44		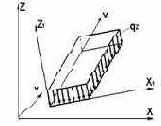	16	Z UX UY	qz(m/м2) mx(mм /n.м) my(mм /n.м)
1	2	3	4	5	6
11,12,21,22,23,24,27,30,41,42,44,			88	0	t, Dt, a
21.22.23,24,27,30				X Z	t, Dt, a1 t, Dt, a2
11,12				UX UY	t, Dt, a1 t, Dt, a2
41,42, 44				X,UX Y,UY	t, Dt, a1 t, Dt, a2

Содержание раздела